Riemann toplamı

Matematikte, Riemann toplamı genellikle fonksiyon eğrisinin altında kalan bölgenin yaklaşık alanıdır. Bu toplama, Alman matematikçi Bernhard Riemann'ın soyadı verilmiştir.

Toplama işlemi, bölgenin farklı şekillere bölünüp (dikdörtgenler ya da yamuklar) birlikte, fonksiyonun ölçülen bölgesine benzer bir alan çıkartılması, ardından da her bir şeklin alanının hesaplanması ve son olarak bütün bu küçük alanların toplanmasından oluşur. Böyle bir uzlaşım belirli integrallerin sayısal hesaplanmasında kullanılabilir. Ayrıca hesabın temel teoremi kapalı tür integral yazımına izin vermediği zaman da kullanılabilir.

Küçük şekillerle doldurulmuş bölgenin alanı tam olarak, ölçülmek istenen alana eşit olmadığı için Riemann toplamı gerçek alandan daha farklı çıkar. Bu hata, bölgeyi daha da küçük şekillere bölmekle giderilebilir. Şekiller küçüldükçe toplam, Riemann integraline yaklaşır.

Tanım

f : D → R fonksiyonunu reel sayılar, R, kümesinin D altkümesinde tanımlayalım. I = [a, b] ise D altkümesinde tanımlı kapalı bir aralık olsun ve

${\displaystyle P=\left\{[x_{0},x_{1}],[x_{1},x_{2}],\dots ,[x_{n-1},x_{n}]\right\},}$

olarak I aralığının bir kesiti olsun ve de

${\displaystyle a=x_{0}<x_{1}<x_{2}<\cdots <x_{n}=b.}$ olsun.

f fonksiyonun I altkümesindeki P kesiti Riemann toplamı şöyle tanımlanır:

${\displaystyle S=\sum _{i=1}^{n}f(x_{i}^{*})(x_{i}-x_{i-1}),\quad x_{i-1}\leq x_{i}^{*}\leq x_{i}.}$

Burada şuna dikkat edilmelidir ki, ${\displaystyle x_{i}^{*}}$ değeri, ${\displaystyle [x_{i-1},x_{i}]}$ aralığında isteğe bağlı bir değerdir, yani herhangi bir f fonksiyonu için farklı Riemann toplamları üretilebilir, yeter ki ${\displaystyle x_{i-1}\leq x_{i}^{*}\leq x_{i}}$ şartı sağlansın.

Örnek: ${\displaystyle x_{i}^{*}}$nin değişik seçimleri, farklı Riemann toplamları verir:

• Eğer, bütün i değerleri için ${\displaystyle x_{i}^{*}=x_{i-1}}$ ise, o zaman S sol Riemann toplamı olur.
• Eğer, bütün i değerleri için ${\displaystyle x_{i}^{*}=x_{i}}$ ise, o zaman S sağ Riemann toplamı olur.
• Eğer, bütün i değerleri için ${\displaystyle x_{i}^{*}={\tfrac {1}{2}}(x_{i}+x_{i-1})}$ ise, o zaman da S orta değer Riemann toplamı olur.
• Sol ve sağ Riemann toplamlarının ortalaması ise yamuklu toplama olur.
• Eğer şöyle bir ifade verilmişse

${\displaystyle S=\sum _{i=1}^{n}v_{i}(x_{i}-x_{i-1}),}$

burada ${\displaystyle v_{i}}$, ${\displaystyle [x_{i-1},x_{i}]}$ aralığında f fonksiyonunun supremum noktasıysa, o zaman S üstten Riemann toplamı olur.

• Benzer şekilde, eğer ${\displaystyle v_{i}}$, ${\displaystyle [x_{i-1},x_{i}]}$ aralığında f fonksiyonunun infimum noktasıysa, o zaman da S alttan Riemann toplamı olur.

Verilen bir kesitteki herhangi bir Riemann toplamı (yani, ${\displaystyle x_{i}^{*}}$ için ${\displaystyle x_{i-1}}$ ve ${\displaystyle x_{i}}$ aralığındaki istenilen değeri) üstten ve alttan Rieman toplamlarının arasında kalır. Riemann integrallenmesi için kesit daraldıkça alttan ve üstten Riemann toplamlarının birbirine hep yaklaşması gerekir. Bu bilgi sayısal integral hesabı için kullanılabilir.

Yöntemler

x³ fonksiyonunun [0,2] aralığındaki Riemann toplama yöntemleri. Dört kesit kullanılarak yapılmıştır.

Sol

Sağ

Orta

Yamuklu

Simpson yöntemi ile

Riemann toplamının dört ana yöntemi, eşit kesit boyutları kullanılarak daha iyi anlaşılabilir. Yani, [a, b] aralığı n alt aralığa bölünür ve her bir aralığın uzunluğu

${\displaystyle \Delta x={\frac {b-a}{n}}.}$

bağıntısıyla bulunur. Kesitlerdeki noktalar da

${\displaystyle a,a+\Delta x,a+2\Delta x,\ldots ,a+(n-2)\Delta x,a+(n-1)\Delta x,b.}$

ile gösterilir.

Sol Riemann Toplamı

Sol toplam, dikdörtgenlerin sol uç noktalarının kullanılması ve Δx taban uzunluğu ile f(a + iΔx) dikdörtgen uzunluğu kullanılmasıyla hesaplanır. Bunu i = 0, 1, ..., n − 1 için yapıp çıkan alanları toplamak şu sonucu verir:

${\displaystyle \Delta x\left[f(a)+f(a+\Delta x)+f(a+2\Delta x)+\cdots +f(b-\Delta x)\right].}$

Eğer f fonksiyonu bu aralıkta monoton azalan bir şekildeyse sol Riemann toplamı gerçek değerden fazla bir sonuca götürür, fakat monoton artan ise gerçek değerden daha düşük bir sonuç çıkartır.

Sağ Riemann Toplamı

Burada f fonksiyonun sağ sınır noktaları kullanılır. Bu da tabanı Δx olan ve yüksekliği f(a + iΔx) olan dikdörtgenler verir. Bu işlemi bütün i = 1, ..., n değerleri için yapmak ve çıkan sonuçları toplamak şunu verir

${\displaystyle \Delta x\left[f(a+\Delta x)+f(a+2\Delta x)+\cdots +f(b)\right].}$

Eğer f fonksiyonu monoton azalansa sağ Riemann toplamı gerçek değerden daha düşük bir sonuç verir, eğer monoton artansa da gerçek değerden daha büyük bir değer verir. Bu formüldeki hata şöyle bulunur

${\displaystyle \left\vert \int _{a}^{b}f(x)\,dx-A_{\mathrm {sag} }\right\vert \leq {\frac {M_{1}(b-a)^{2}}{2n}},}$

burada ${\displaystyle M_{1}}$, ${\displaystyle f^{\prime }(x)}$ fonksiyonun mutlak değerinin o aralıktaki maksimum değeridir.

Orta Değer Riemann Toplamı

f fonksiyonunu, aralığın orta noktalarını kullanarak, boyları, birinci aralık için f(a + Q/2), ikincisi için f(a + 3Q/2) olan ve f(b − Q/2) kadar giden dikdörtgenler verir. Bunların alan toplamları şöyledir

${\displaystyle Q\left[f(a+{\tfrac {Q}{2}})+f(a+{\tfrac {3Q}{2}})+\cdots +f(b-{\tfrac {Q}{2}})\right].}$

Bu formülün hatası şöyledir

${\displaystyle \left\vert \int _{a}^{b}f(x)\,dx-A_{\mathrm {orta} }\right\vert \leq {\frac {M_{2}(b-a)^{3}}{24n^{2}}},}$

burada ${\displaystyle M_{2}}$, ${\displaystyle f^{\prime \prime }(x)}$ fonksiyonun mutlak değerinin o aralıktaki maksimum değeridir.

Yamuklu Toplama Kuralı

Bu yöntemde ise, f fonksiyonunun aralıktaki değerleri sol ve sağ sınır noktalarının ortalamasına denkleştirilir. Yukarıdakilerle aynı olarak, yamuk için alan formülünü kullanarak

${\displaystyle A={\tfrac {1}{2}}h(b_{1}+b_{2})}$

b₁, b₂ paralel kenarlı ve h yükseklikli yamukların alanını hesaplayıp şu formülle bütün bu alanları toplamak mümkün olur

${\displaystyle {\tfrac {1}{2}}Q\left[f(a)+2f(a+Q)+2f(a+2Q)+2f(a+3Q)+\cdots +f(b)\right].}$

Bu formüldeki hata şöyle hesaplanır

${\displaystyle \left\vert \int _{a}^{b}f(x)\,dx-A_{\mathrm {yamuk} }\right\vert \leq {\frac {M_{2}(b-a)^{3}}{12n^{2}}},}$

burada da ${\displaystyle M_{2}}$, ${\displaystyle f^{\prime \prime }(x)}$ fonksiyonun mutlak değerinin o aralıktaki maksimum değeridir.

Yamuk yöntemiyle hesaplanan olası alan değeri sağ ve sol toplamların ortalamasına eşittir.

Örnek

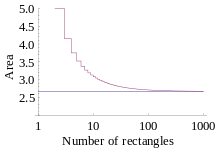
Örnek olarak, y = x² fonksiyonunun 0 ile 2 arasındaki eğri altında kalan alanı Riemann toplamı kullanılarak algoritmik bir şekilde hesaplanabilir.

İlk önce, [0, 2] aralığı n parçaya bölünür ve her birinin genişliği ${\displaystyle {\tfrac {2}{n}}}$ kadardır; bunlar Riemann dikdörtgenlerinin (bu noktadan sonra "kutu" denilecek) enleridir. Sağ Riemann toplamı kullanılacağı için, kutuların x koordinatları dizisi ${\displaystyle x_{1},x_{2},\ldots ,x_{n}}$ şeklinde olur. Aynı şekilde, kutuların uzunluk dizisi de ${\displaystyle x_{1}^{2},x_{2}^{2},\ldots ,x_{n}^{2}}$ olur. ${\displaystyle x_{i}={\tfrac {2i}{n}}}$, ${\displaystyle x_{n}=2}$ eşitliklerini göz önünde bulundurmak önemlidir.

Her kutunun alanı ${\displaystyle {\tfrac {2}{n}}\times x_{i}^{2}}$ olur ve de ninci sağ Riemann toplamı:

${\displaystyle {\begin{aligned}S&={\frac {2}{n}}\times \left({\frac {2}{n}}\right)^{2}+\cdots +{\frac {2}{n}}\times \left({\frac {2i}{n}}\right)^{2}+\cdots +{\frac {2}{n}}\times \left({\frac {2n}{n}}\right)^{2}\\&={\frac {8}{n^{3}}}\left(1+\cdots +i^{2}+\cdots +n^{2}\right)\\&={\frac {8}{n^{3}}}\left({\frac {n(n+1)(2n+1)}{6}}\right)\\&={\frac {8}{n^{3}}}\left({\frac {2n^{3}+3n^{2}+n}{6}}\right)\\&={\frac {8}{3}}+{\frac {4}{n}}+{\frac {4}{3n^{2}}}\end{aligned}}}$

olur.

Eğer n → ∞ iken, yukarıdaki toplama formülünün limiti alınırsa, artan kutuların alan toplamı değerinin, grafiğin altında kalan bölgenin gerçek alanına yaklaştığı fark edilir. Dolayısıyla:

${\displaystyle \lim _{n\to \infty }S=\lim _{n\to \infty }\left({\frac {8}{3}}+{\frac {4}{n}}+{\frac {4}{3n^{2}}}\right)={\frac {8}{3}}}$

Bu yöntem daha farklı yollarla hesaplanan belirli integral ile de uyuşmaktadır:

${\displaystyle \int _{0}^{2}x^{2}\,dx={\frac {8}{3}}}$

Animasyonlar

• 
  Sol Toplam
• 
  Sağ Toplam
• 
  Orta Değer Toplamı
• 
  ${\displaystyle y=x^{2}}$ fonksiyonu için

Daha Fazlası

• Riemann integrali
• Riemann–Stieltjes integrali
• Lebesgue integrali
• Simpson Yöntemi
• Euler yöntemi and ortanokta yöntemi, diferansiyel denklem çözümüyle alakalı bazı yöntemler.

Kaynakça

• Thomas, George B. Jr.; Finney, Ross L. (1996), Calculus and Analytic Geometry (9th ed.), Addison Wesley, ISBN 0-201-53174-7 

Dış bağlantılar

• Riemann toplamlarının yakınsamasını gösteren bir simülasyon19 Şubat 2015 tarihinde Wayback Machine sitesinde arşivlendi.